Selection Steps

1. Determine system (machinery/ application).
2. Determine operating mode (speed, acceleration/deceleration time, positioning time).
3. Calculate speed of rotation (n), inertia (J) and torque (T).
4. Select a motor temporarily.
   • The inertia of the selected servo motor is more than a certain ratio of a load Inertia.
     

     Load/Motor inertia ratio	Option 1	Option 2	Option 3
     Closed loop stepping motor	50	100	200
     Stepping motor	30	40	50
     DC brushed servomotor	3	5	10
     DC brushless servomotor	3	5	10
     DC brushless torque motor	10	20	30

     Note: For large inertia (> 20kg∙m²), DC brushed motors and DC brushless motors usually use ratio of 3 or 5.
   • 80% of the Rated Torque of the selected servo motor is more than the load torque of the servomotor shaft conversion value.
5. Calculate additional acceleration/deceleration torque (M_A).
6. Calculate maximum momentary torque and calculate effective torque
   Acceleration torque (N∙m): \(M_1=M+M_A\)
   Uniform torque (N∙m): \(M_2=M\)
   Deceleration torque (N∙m): \(M_3=M-M_A\)
   Effective torque/Root mean square torque (N∙m): $$M_{RMS} = \sqrt{\frac {1} {\left(t_1+t_2+\cdots+t_n\right)} \left (t_1 \cdot {M_1}^2+t_2 \cdot {M_2}^2+ \cdots +t_n \cdot {M_n}^2\right)}$$
7. Confirm motor selection requirements and verify selected motor.
   The maximum torque of the motor is larger than M₁;
   The rated torque of the motor is larger than M and M_RMS;
   The rated speed of the motor is larger than n.
8. Rated torque and maximum torque should be calculated if required.

Power and Torque

The relationship between power and torque is: $$M=9550\cdot\frac{P}{n}$$ where
M: Torque (N∙m)
P: Power (kW)
n: Speed of Rotation (rpm)

Also, power can be calculated by： $$P=F\cdot v$$ where
F: Force (N)
v: Velocity (m/s)

In many cases, when force is friction force: $$F=\mu mg$$ where
µ: Friction Coefficient (N∙m)
m: Mass (m/s)
g: Gravity Acceleration (m/s²)

External force is positive when it is against the direction of operation.

Formulas for different machinery

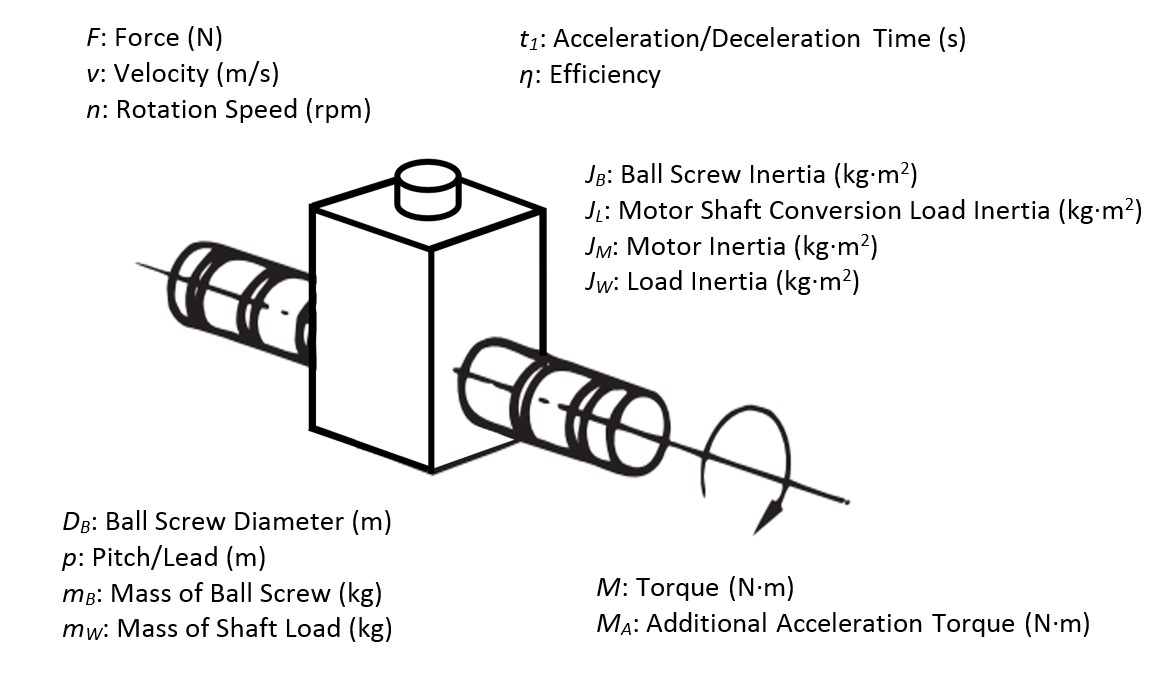
Screw		Speed of Rotation	$$n=\frac{60}{p}\cdot v$$
		Inertia	$$J_B={\frac{1}{8}\cdot m}_B\cdot{D_B}^2$$ $$J_W=m_W\cdot\left(\frac{p}{2\pi}\right)^2$$ $$J_L=J_B+J_W$$
		Torque	$$M=F\cdot\frac{p}{2\pi\eta}$$ $$M_A=\frac{2\pi n}{60t_1}\cdot\left(\frac{J_L}{\eta}+J_M\right)$$
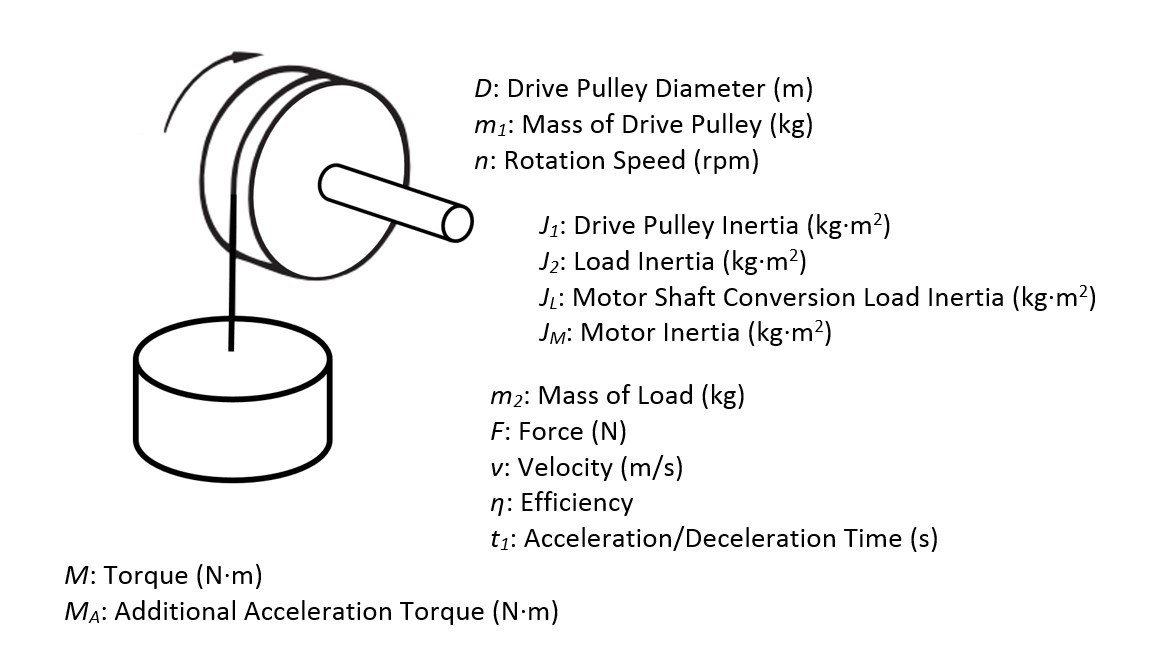
Lift		Speed of Rotation	$$n=\frac{60}{\pi D}\cdot v$$
		Inertia	$$J_1=\frac{m_1D^2}{8}$$ $$J_2=\frac{m_2D^2}{4}$$ $$J_L=J_1+J_2$$
		Torque	$$M=F\cdot\frac{D}{2\eta}$$ $$M_A=\frac{2\pi n}{60t_1}\cdot\left(\frac{J_L}{\eta}+J_M\right)$$
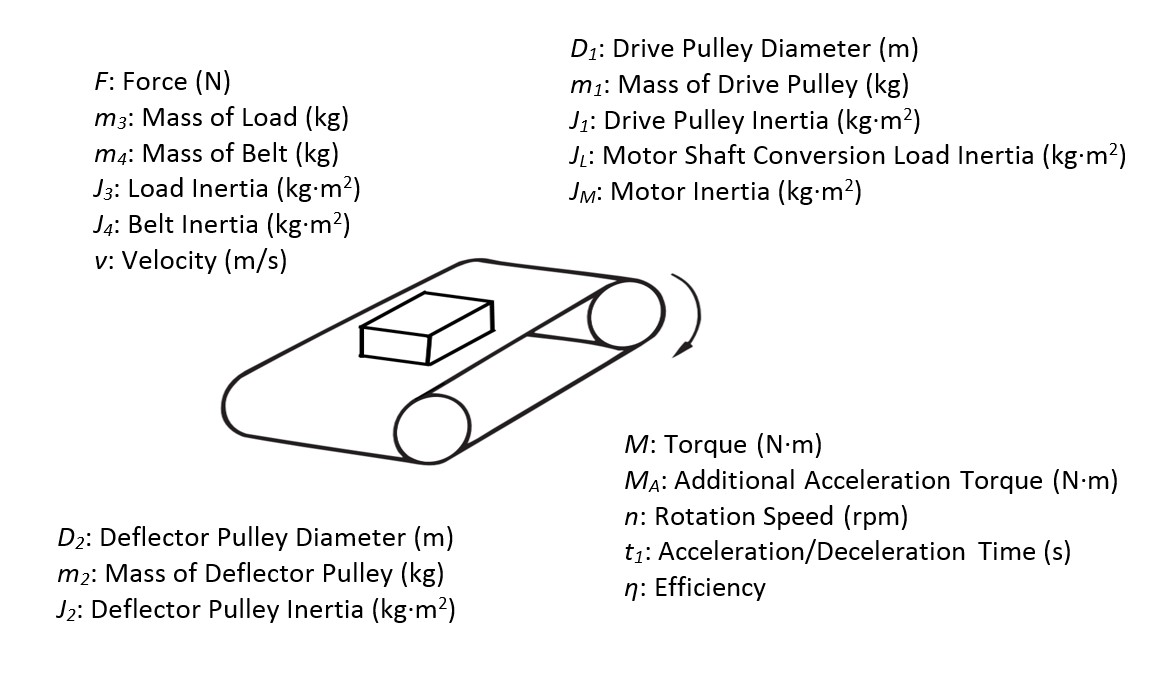
Belt		Speed of Rotation	$$n=\frac{60}{{\pi D}_1}\cdot v$$
		Inertia	$$J_1=\frac{m_1{D_1}^2}{8}$$ $$J_2=\frac{m_2{D_2}^2}{8}\cdot\frac{{D_1}^2}{{D_2}^2}$$ $$J_3=\frac{m_3{D_1}^2}{4}$$ $$J_4=\frac{m_4{D_1}^2}{4}$$ $$J_L=J_1+J_2+J_3+J_4$$
		Torque	$$M=F\cdot\frac{D_1}{2\eta}$$ $$M_A=\frac{2\pi n}{60t_1}\cdot\left(\frac{J_L}{\eta}+J_M\right)$$
Rack and Pinion		Speed of Rotation	$$n=\frac{60}{pz}\cdot v$$
		Inertia	$$J_W=m_W\cdot\left(\frac{pz}{2\pi}\right)^2$$ $$J_L=J_P+J_W$$
		Torque	$$M=F\cdot\frac{pz}{2\pi\eta}$$ $$M_A=\frac{2\pi n}{60t_1}\cdot\left(\frac{J_L}{\eta}+J_M\right)$$
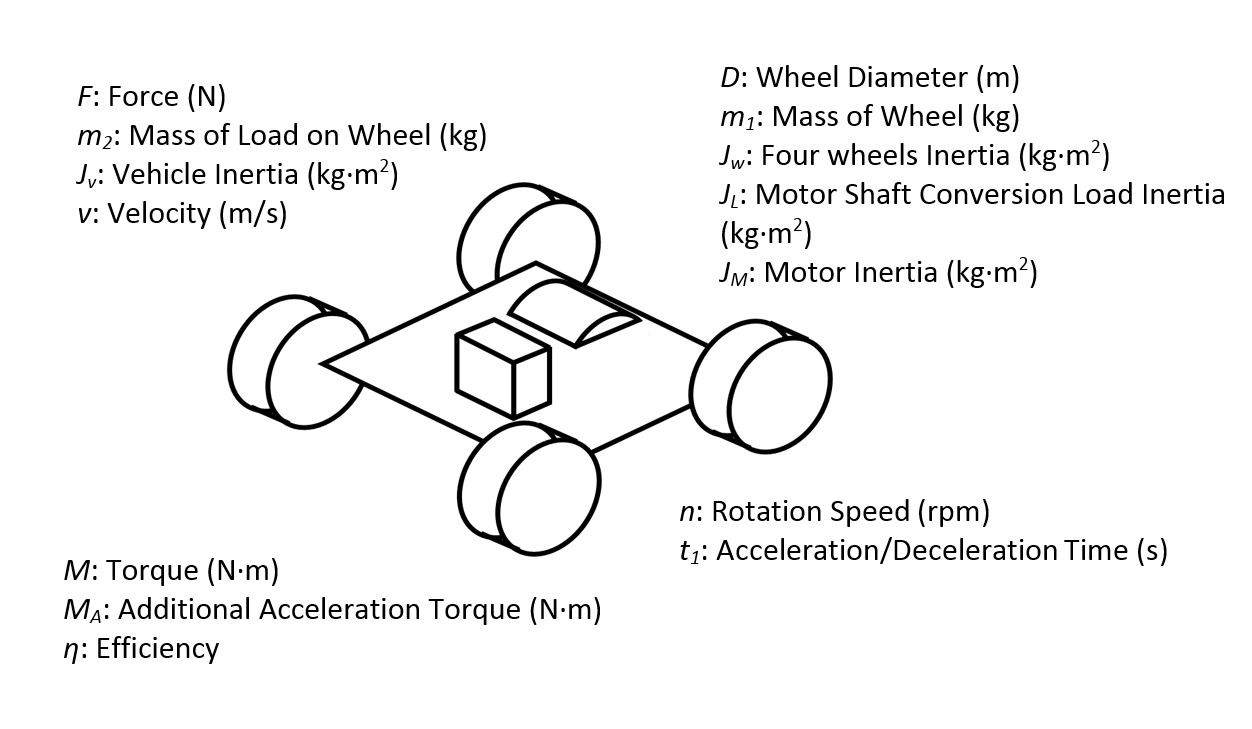
Four-Wheel Vehicle		Speed of Rotation	$$n=\frac{60}{\pi D}\cdot v$$
		Inertia	$$J_W=\frac{1}{8}\cdot m_1\cdot D^2\cdot4$$ $$J_V=m_2\cdot\left(\frac{D}{2}\right)^2$$ $$J_L=J_W+J_V$$
		Torque	$$M=F\cdot\frac{D}{2\eta}$$ $$M_A=\frac{2\pi n}{60t_1}\cdot\left(\frac{J_L}{\eta}+J_M\right)$$
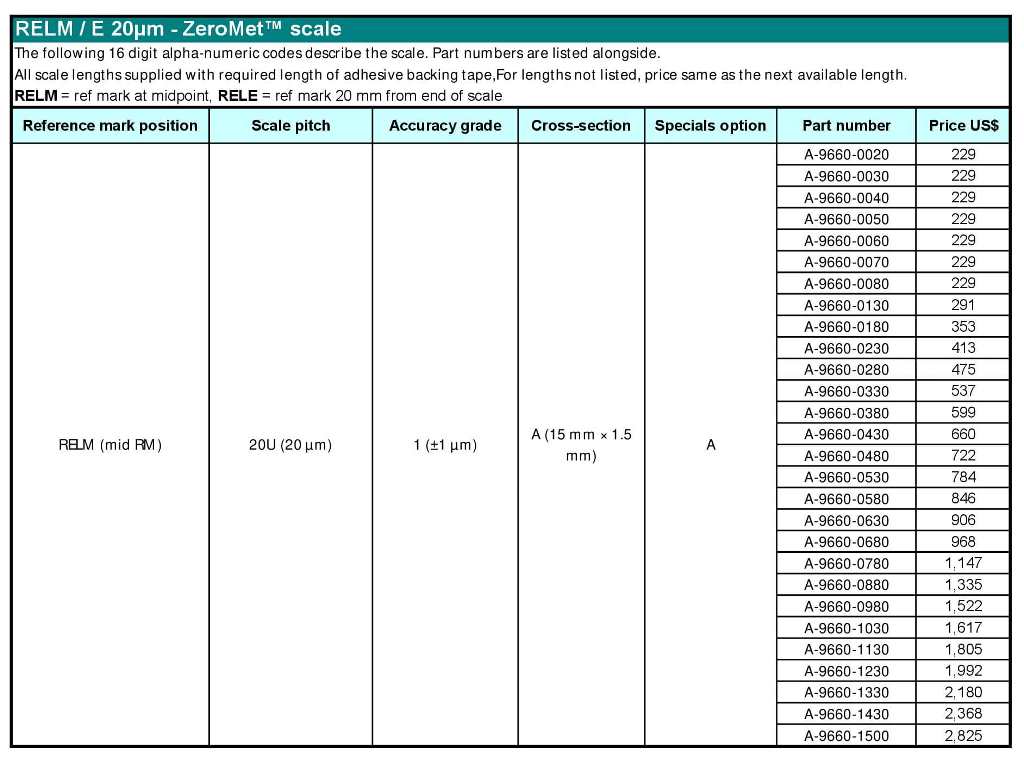
Table		Speed of Rotation	$$n$$
		Inertia	$$J_1=\frac{1}{8}\cdot m_1\cdot{D_1}^2$$ $$J_2=\frac{1}{8}\cdot m_2\cdot{D_2}^2$$ $$J_3=\frac{1}{8}\cdot m_3\cdot{D_3}^2+m_3\cdot r^2$$ $$J_L=J_1+J_2+J_3$$
		Torque	$$M=F\cdot\frac{d}{\eta}$$ $$M_A=\frac{2\pi n}{60t_1}\cdot\left(\frac{J_L}{\eta}+J_M\right)$$